
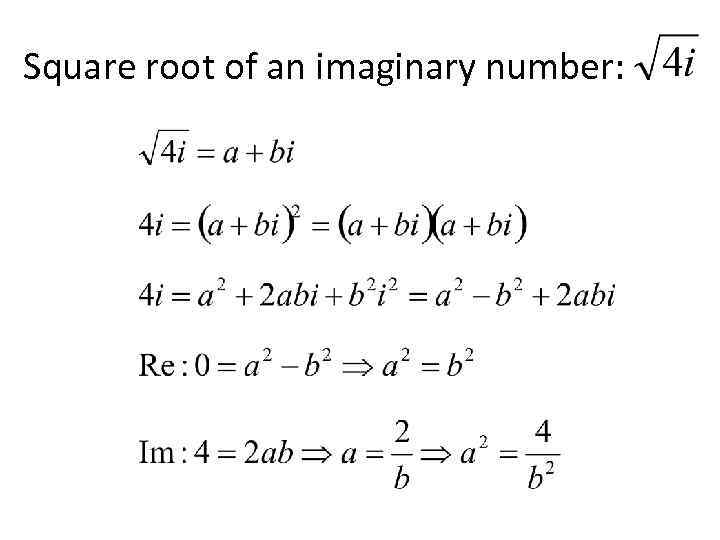

The square root of x is rational if and only if x is a rational. (Why this isn’t z.arg() is a mystery to me.)Īs you’ll notice, Sage is remarkably bad at doing this symbolically: it just sort of throws up its hands at 1+sqrt(3)i, where we (of course) know the answer is pi/3. In geometrical terms, the square root function maps the area of a square to its side length. The angle is the argument, so use arg(z).
Square root of complex number how to#
If we want to convert rectangular representations of complex number to polar ones, we already know how to get the length, with z.abs(). The imaginary number i is defined as the square root of 1. You can also use exponential (or polar) notation for complex numbers. If the value in the radicand is negative, the root is said to be an imaginary number.

We can get around this by using the identity above: (The “bool” means we want to know if the expression is true or false, i.e., we want a “ boolean“.) Sage (reasonably) calls this the “absolute value”: Lets compare coeffiecients to obtain two. The norm of a complex number a+bi is sqrt(a^2+b^2). How do you find the square roots of a complex number Lets consider the complex number 21-20i. When a single letter is used to denote a complex number, it is sometimes called an ' affix. Sometimes you want to extract the real part or the imaginary part of a complex number: The complex numbers are the field of numbers of the form, where and are real numbers and i is the imaginary unit equal to the square root of . For finding the square root of a positive real number, we can use the otherwise called, exponent operator as mentioned here, but for negative or complex. In the following description, (z) stands for the complex number and (z) for the absolute value. In contexts in which use of the letter i is ambiguous or problematic, the letter j is sometimes used instead. (This choice is because “i” is often used as an index, as in “for i=1…5”.) Manipulations work as you would expect: Square root formula for a complex number. In practice, square roots of complex numbers are more easily found by rst converting to polar form and then using DeMoivres Theorem. There are two complex square roots of 1: and, just as there are two complex square roots of every real number other than zero (which has one double square root ). Note that Sage uses “I” to stand for i, the square root of -1. X = ± √) = ± (√32/2 - i √18/2) = ± (4 - 3i).This week, the main new computational topic is complex eigenvalues and eigenvectors. Sage finds complex eigenvalues / eigenvectors by default, so we already know how to find complex eigenvectors: Assume the complex number : Now, let us derive the formula to find the square root of a complex number a. Now, we have x 2 + y 2 = √(a 2 + b 2) and a = x 2 - y 2. To find the square root of a complex number: Step1. ⇒ a + ib = x 2 - y 2 + i2xy Ĭomparing real and imaginary parts of the above equation, we have The calculation of roots of complex numbers is the process of finding the roots (square, cube, etc.) Finding square roots of complex numbers can be achieved. Now squaring both sides of the equation, we have Assume the square root of complex number a + ib to be x + iy, that is, √(a + ib) = x + iy. Now, let us derive the formula to find the square root of a complex number a + ib. 2 1(2+2i) Find the square root of the following complex numbers: 86i Find the square root of the following complex number: 1+43 Find the square.


 0 kommentar(er)
0 kommentar(er)
